Signals are wave frequency. Signals convey transfer some information in the form of waves and packets particle. Signal have arbitrary amplitude profile and it is difficult to analyze them in that from therefore it is necessity to decompose signals in terms of simple and mathematically well defined basic signals.
In today's world is replete with many examples of singles available for processing or analysis. Lets discuss on business section of your daily or weekly paper and note the stock market(share market) averages plotted daily, weekly, or monthly over the past year data.
In hospitals doctor’s office for our annual checkup and note the printout of the electrocardiogram (ECG) and in some cases, the electroencephalogram (EEG) taken by the doctor or nurse. This data representation done by signal propagation.
In sports game large database graph representation of many players plotted match by match, monthly performance done by signal processing system.
These are countless examples of measured data that vary with time represent the signal we shall be discussing in this blog. The data or information in question, besides varying in time, may be random or unpredictable and will generally be carrying some useful information that is to be extracted automatically by computer. This is processing activity mentioned above.
The data points maybe digital (discrete numbers) or continuously varying (Analog Signal).
Signals Classification
According to graph representation signals are classified in three forms like – continuous signals, Discrete signals, Digital Signals.
Continuous Signals –
A signals are call continuous signals if signal defined in the form of x(t) for all instance of time t.
F(x) = x (t)
This F(x) function is called continuous function.
Discrete Signals –
A signal performs discrete signals when signal vary time to time and not propagate in all time interval is called discrete signals. It define or representation in mathematical form is –
F(x) = x (nt)
Where
t = is defined under discrete sampling time interval.
n = an Integer value.
Now if we assume that the sampling interval is uniform sampling a continuous-time signal is the most common way of generating the discrete signal.
Digital Signal –
A digital signal, which is actually used in practical signal processing with digital devices, has both its dependent and independent variables in discrete form.
Simple Signals-
There are many ways in which signals can be classified or characterized. We have already distinguished between Analog, digital, and discrete-time signals.
Some – sample signals function are-
1- Constant function – Xn =C0 (any constant)
2- Straight Line – Xn = C0 + C1n
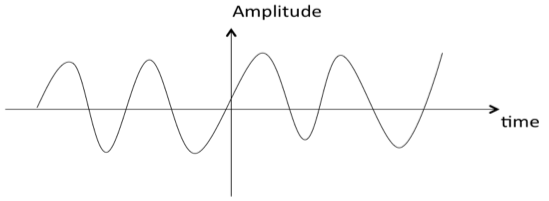
3- Sinusoid – Xn = αcos(ßn +γ)
4- Exponential – Xn = μeλn
Signals propagate in medium and environment noise also propagate together. That's why some Amplitude, Pich, and others signals factors differ form the original signal, again we receive same signal. Use electronic tools like a low pass filter, high pass filter, Amplifier and many more.




0 Comments